백준 1074번) Z JAVA
https://www.acmicpc.net/problem/1074
1074번: Z
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다. N > 1인 경우, 배열을
www.acmicpc.net
#문제
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다.
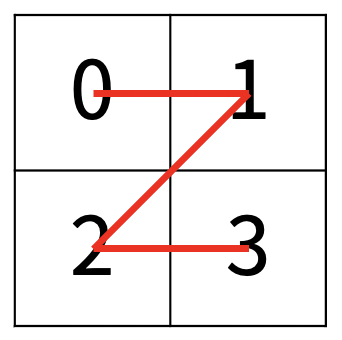
N > 1인 경우, 배열을 크기가 2N-1 × 2N-1로 4등분 한 후에 재귀적으로 순서대로 방문한다.
다음 예는 22 × 22 크기의 배열을 방문한 순서이다.
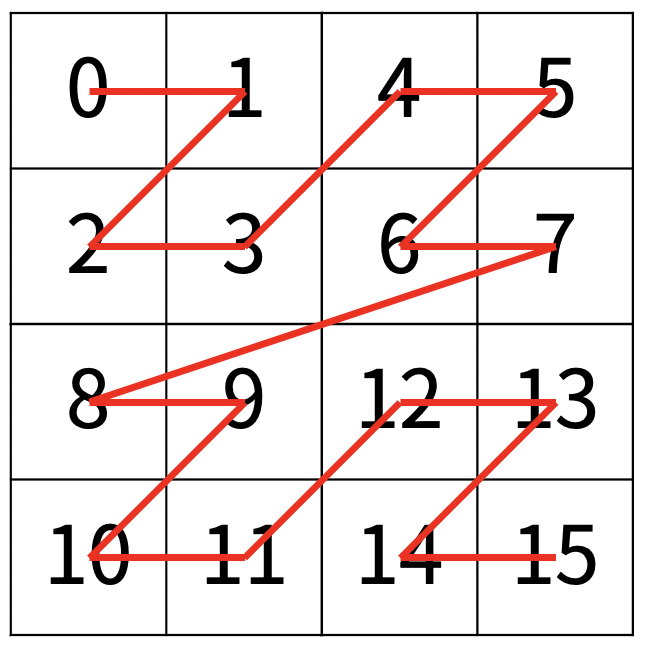
N이 주어졌을 때, r행 c열을 몇 번째로 방문하는지 출력하는 프로그램을 작성하시오.
다음은 N=3일 때의 예이다.

#알고리즘
분할정복, 재귀
#난이도
SIlver 1
#풀이방법
정말 오랜만에 쓰는 알고리즘 풀이인 것 같다. 시험기간이라는 핑계(?)로 3주동안 알고리즘 문제 및 프로젝트를 진행하지 못했다...ㅠㅠ
분할 정복?, 간간히 접한 문제긴 하지만 다른 알고리즘 유형보다는 확실히 덜 익숙한 유형이다.
처음에 이 문제를 접했을때부터 실버1 문제임에도 불구하고 어디서부터 손을 대야할지 막막했다...
따라서 구글링을 통해 분할정복이라는 알고리즘 유형을 공부한다음 이 문제를 접근했다.
배열의 크기는 2의 제곱으로 나뉜다. n이 3이라면 2의 3의 제곱 , n이 5라면 2의 5제곱 등등.. n의 크기에 따라
배열의 크기가 결정됐는데.. 문제를 풀때 배열을 선언한 것 부터 자체가 메모리 초과가 되었다. 어떻게 하면 메모리 초과 문제를 해결 할 수 있을지 고민하다가 생각해보니 굳이 배열을 선언할 필요가 있을까?... 라는 생각이 들었다.
중요한 것은 r과 c가 몇번째 거치는 것을 알고 싶은 것인지 쓸데 없이 배열을 선언해서 2의 제곱 X 2의 제곱이라는 엄청난 메모리를 할당할 필요가 없었다. 코드를 짤 때 중요한 것은 내가 어떤 것을 원하는가가 중요한 것인지 이것저것
있어보이게(?) 코드를 짤 필요가 없었다. 필요한 핵심만 골라서 딱딱 찾으면 문제 해결 ? 끝!
4구간으로 나누어 stack처럼 재귀함수처럼
public static void conquer(int n,int r,int c) {
if(n == 0) {
if(r == goal_r && c == goal_c) {
System.out.println(count);
System.exit(0);
}
count++;
return;
}
conquer(n-1,r,c);
conquer(n-1,r,c+(int)Math.pow(2,n)/2);
conquer(n-1,r+(int)Math.pow(2,n)/2,c);
conquer(n-1,r+(int)Math.pow(2,n)/2,c+(int)Math.pow(2,n)/2);
}
4구간으로 나누어 함수를 재귀적으로 호출할때 parameter 값으로 n-1씩 2의 제곱을 줄여 나가 차근 차근 함수를 호출한다. 함수를 호출하는 순서는
1 2
3 4
1번 -> 2번 -> 3번 -> 4번
(2 x 2)인 경우,
| 1 | 2 |
| 3 | 4 |
(4 X 4)인 경우
| 1 | 2 | 1 | 2 |
| 3 | 4 | 3 | 4 |
| 1 | 2 | 1 | 2 |
| 3 | 4 | 3 | 4 |
제일 큰 구간을 4구간으로 나누고, 또 그 1번을 다시 4구간으로 나누고
재귀적으로 DFS마냥 호출하여 센다
구간을 지나면 count++하여 횟수를 늘려준다.
goal_r == r && goal_c == c
이면 이 횟수를 출력한다.
그런데 이게 웬일??
시간초과가 나버렸다....
n이 15까지 있어 2의 15제곱이 있다면 양이 매우 많이 시간 초과가 나버린 것인다.
어떻게 하면 시간초과를 해결 할 수 있을까? 고민하다가 4구간이 있다면 구간마다 범위가 계속 정해져있을텐데
r과 c가 구간의 범위 안에 있을 경우, 그 함수를 호출 한다.
또한 범위가 아닌 경우 그 범위에 있는 부분을 모두 count에 더해준다.
이렇게 할 경우 범위가 out된 부분은 쓸데없이 일일이 세줄 필요 없이 더해주고 범위에 있는 부분만 count에 더해줘
주어진 시간 내에 빠르게 count할 수 있게 된다.
#코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 | import java.util.*; //1t, 시간 초과 -> public class Main { static int N; static int goal_r; static int goal_c; static int count = 0; public static void conquer(int n,int r,int c) { if(n == 0) { if(r == goal_r && c == goal_c) { System.out.println(count); System.exit(0); } count++; return; }//한칸인 경우 갯수 세기 if((r <= goal_r && goal_r < r+(int)Math.pow(2,n)/2) && (c <= goal_c && goal_c < c+(int)Math.pow(2,n)/2)){ conquer(n-1,r,c); }//만약 목표가 1번구간에 있다면 호출 count += (int)Math.pow(2,n-1) * (int)Math.pow(2,n-1); //1번 구간 생략 -> 더해줌 if((r <= goal_r && goal_r < r+(int)Math.pow(2,n)/2) && (c+(int)Math.pow(2,n)/2) <= goal_c && goal_c < c+(int)Math.pow(2,n)) { conquer(n-1,r,c+(int)Math.pow(2,n)/2); }//만약 목표가 2번구간에 있다면 호출 count += (int)Math.pow(2,n-1) * (int)Math.pow(2,n-1); //2번 구간 생략 -> 더해줌 if((r+(int)Math.pow(2,n)/2 <= goal_r && goal_r < r+(int)Math.pow(2,n)) && (c <= goal_c && goal_c < c+(int)Math.pow(2,n)/2)) { conquer(n-1,r+(int)Math.pow(2,n)/2,c); }//만약 목표가 3번구간에 있다면 호출 count += (int)Math.pow(2,n-1) * (int)Math.pow(2,n-1); //3번 구간 생략 -> 더해줌 if((r+(int)Math.pow(2,n)/2 <= goal_r && goal_r < r+(int)Math.pow(2,n)) && (c+(int)Math.pow(2,n)/2) <= goal_c && goal_c < c+(int)Math.pow(2,n)) { conquer(n-1,r+(int)Math.pow(2,n)/2,c+(int)Math.pow(2,n)/2); }//만약 목표가 4번구간에 있다면 호출 } public static void main(String[] args) { Scanner sc = new Scanner(System.in); N = sc.nextInt(); goal_r = sc.nextInt(); goal_c = sc.nextInt(); conquer(N,0,0); } } | cs |